PdeFiniteDifferenceSolver
C++/CUDA implementation of the most popular hyperbolic and parabolic PDE solvers
Project maintained by pmontalb Hosted on GitHub Pages — Theme by mattgraham
PdeFiniteDifferenceSolver
C++ manager class for PdeFiniteDifferenceKernels API. The low level calls are managed in the namespace pde::detail DeviceManager, whereas the high level infrastructure is delegated to the particular solver type.
Only linear hyperbolic and parabolic PDEs are supported (up to 3D). The exposed implementation is through:
- AdvectionDiffusionSolver1D, AdvectionDiffusionSolver2D
- WaveEquationSolver1D, WaveEquationSolver2D
These solvers are implemented with the Curiously Recurring Template Pattern (CRTP), useful for delegating the members data type at compile time.
For convenience’s sake the following typedefs have been defined:
- Advection-Diffusion:
typedef AdvectionDiffusionSolver1D<MemorySpace::Device, MathDomain::Float> GpuSingleAdvectionDiffusionSolver1D; typedef GpuSingleAdvectionDiffusionSolver1D GpuFloatAdvectionDiffusionSolver1D; typedef AdvectionDiffusionSolver1D<MemorySpace::Device, MathDomain::Double> GpuDoubleAdvectionDiffusionSolver1D; typedef AdvectionDiffusionSolver1D<MemorySpace::Host, MathDomain::Float> CpuSingleAdvectionDiffusionSolver1D; typedef CpuSingleAdvectionDiffusionSolver1D CpuFloatAdvectionDiffusionSolver1D; typedef AdvectionDiffusionSolver1D<MemorySpace::Host, MathDomain::Double> CpuDoubleAdvectionDiffusionSolver1D; typedef GpuSingleAdvectionDiffusionSolver1D ad1D; typedef GpuDoubleAdvectionDiffusionSolver1D dad1D; typedef AdvectionDiffusionSolver2D<MemorySpace::Device, MathDomain::Float> GpuSingleAdvectionDiffusionSolver2D; typedef GpuSingleAdvectionDiffusionSolver2D GpuFloatAdvectionDiffusionSolver2D; typedef AdvectionDiffusionSolver2D<MemorySpace::Device, MathDomain::Double> GpuDoubleAdvectionDiffusionSolver2D; typedef AdvectionDiffusionSolver2D<MemorySpace::Host, MathDomain::Float> CpuSingleAdvectionDiffusionSolver2D; typedef CpuSingleAdvectionDiffusionSolver2D CpuFloatAdvectionDiffusionSolver2D; typedef AdvectionDiffusionSolver2D<MemorySpace::Host, MathDomain::Double> CpuDoubleAdvectionDiffusionSolver2D; typedef GpuSingleAdvectionDiffusionSolver2D ad2D; typedef GpuDoubleAdvectionDiffusionSolver2D dad2D; - Wave Equation:
typedef WaveEquationSolver1D<MemorySpace::Device, MathDomain::Float> GpuSingleWaveEquationSolver1D; typedef GpuSingleWaveEquationSolver1D GpuFloatWaveEquationSolver1D; typedef WaveEquationSolver1D<MemorySpace::Device, MathDomain::Double> GpuDoubleWaveEquationSolver1D; typedef WaveEquationSolver1D<MemorySpace::Host, MathDomain::Float> CpuSingleWaveEquationSolver1D; typedef CpuSingleWaveEquationSolver1D CpuFloatWaveEquationSolver1D; typedef WaveEquationSolver1D<MemorySpace::Host, MathDomain::Double> CpuDoubleSolver1D; typedef GpuSingleWaveEquationSolver1D wave1D; typedef GpuDoubleWaveEquationSolver1D dwave1D; typedef WaveEquationSolver2D<MemorySpace::Device, MathDomain::Float> GpuSingleWaveEquationSolver2D; typedef GpuSingleWaveEquationSolver2D GpuFloatWaveEquationSolver2D; typedef WaveEquationSolver2D<MemorySpace::Device, MathDomain::Double> GpuDoubleWaveEquationSolver2D; typedef WaveEquationSolver2D<MemorySpace::Host, MathDomain::Float> CpuSingleWaveEquationSolver2D; typedef CpuSingleWaveEquationSolver2D CpuFloatWaveEquationSolver2D; typedef WaveEquationSolver2D<MemorySpace::Host, MathDomain::Double> CpuDoubleSolver2D; typedef GpuSingleWaveEquationSolver2D wave2D; typedef GpuDoubleWaveEquationSolver2D dwave2D;
Sample usage - 1D
Advection-Diffusion
cl::vec grid = cl::LinSpace(0.0f, 1.0f, 128);
auto _grid = grid.Get();
std::vector<float> _initialCondition(grid.size());
for (unsigned i = 0; i < _initialCondition.size(); ++i)
_initialCondition[i] = sin(_grid[i]);
cl::vec initialCondition(_initialCondition);
unsigned steps = 100;
double dt = 1e-4;
float velocity = .05f;
float diffusion = 0.1f;
BoundaryCondition leftBoundaryCondition(BoundaryConditionType::Neumann, 0.0);
BoundaryCondition rightBoundaryCondition(BoundaryConditionType::Neumann, 0.0);
BoundaryCondition1D boundaryConditions(leftBoundaryCondition, rightBoundaryCondition);
pde::GpuSinglePdeInputData1D data(initialCondition, grid, velocity, diffusion, dt, solverType, SpaceDiscretizerType::Centered, boundaryConditions);
pde::ad1D solver(data);
solver.Advance(steps);
const auto solution = solver.solution->columns[0]->Get();
Wave Equation
cl::dvec grid = cl::LinSpace<MemorySpace::Device, MathDomain::Double>(0.0, 1.0, 128);
auto _grid = grid.Get();
std::vector<double> _initialCondition(grid.size());
for (unsigned i = 0; i < _initialCondition.size(); ++i)
_initialCondition[i] = sin(_grid[i]);
cl::dvec initialCondition(_initialCondition);
unsigned steps = 100;
double dt = 1e-4;
double velocity = .05;
BoundaryCondition leftBoundaryCondition(BoundaryConditionType::Neumann, 0.0);
BoundaryCondition rightBoundaryCondition(BoundaryConditionType::Neumann, 0.0);
BoundaryCondition1D boundaryConditions(leftBoundaryCondition, rightBoundaryCondition);
pde::GpuDoublePdeInputData1D data(initialCondition, grid, velocity, diffusion, dt, solverType, SpaceDiscretizerType::Centered, boundaryConditions);
pde::dwave1D solver(data);
solver.Advance(steps);
const auto solution = solver.solution->columns[0]->Get();
Sample results - 1D
I wrote a simple python script for plotting the results:
Hyperbolic - first order: transport equation
- Numerical instability of the centered difference scheme (regardless of the time solver) <p align="center">
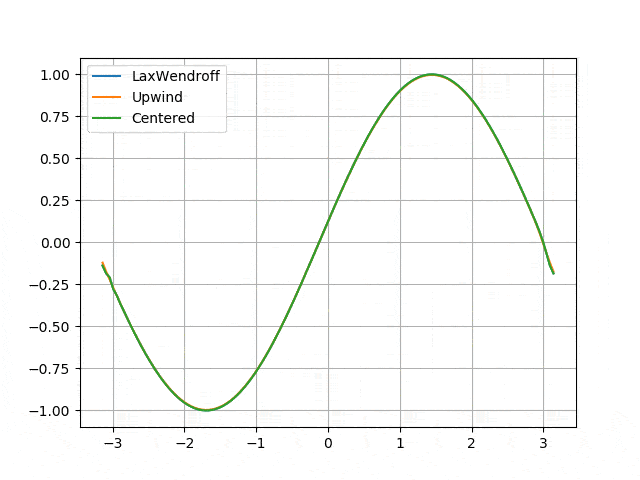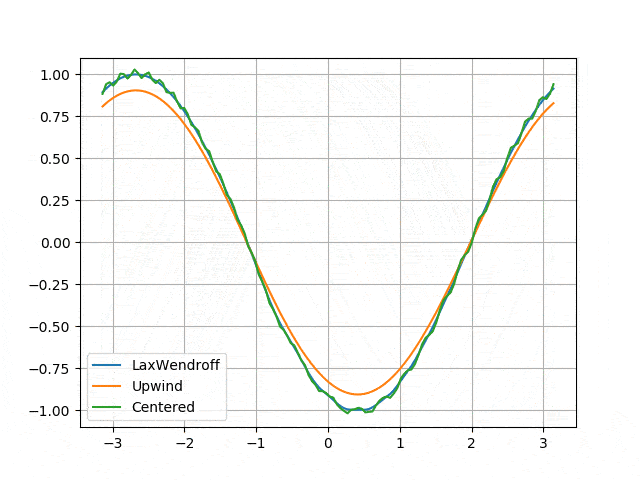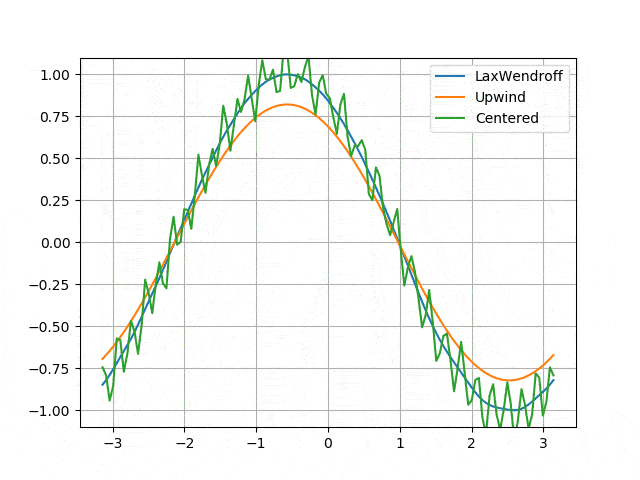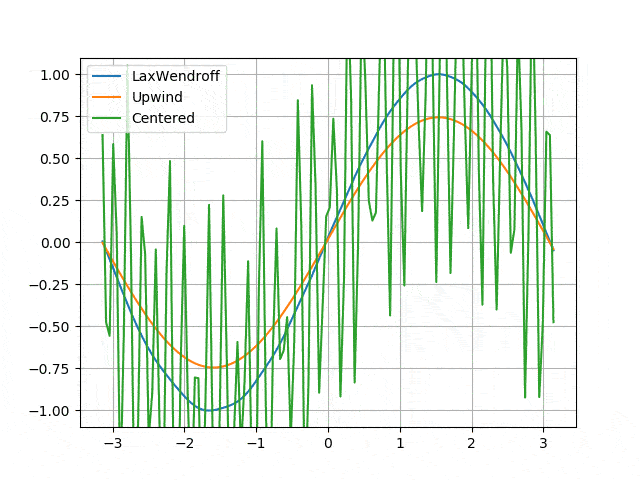 </p>
</p> - Numerical diffusion induced by the Upwind scheme and solved by the Lax-Wendroff scheme <p align="center">
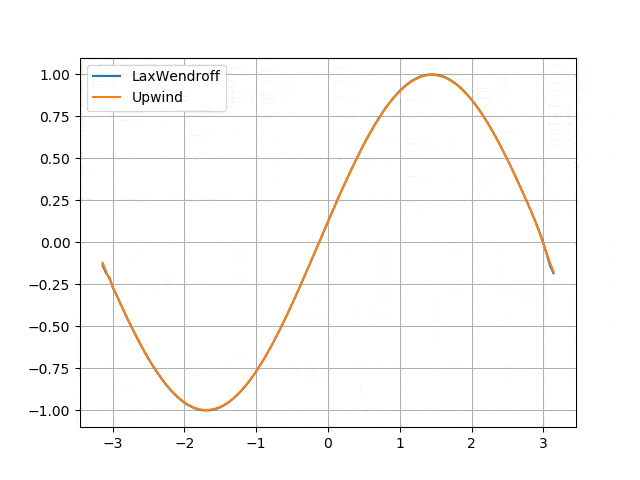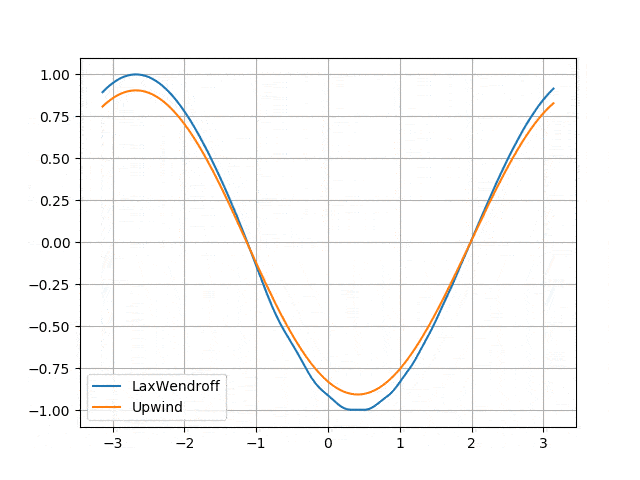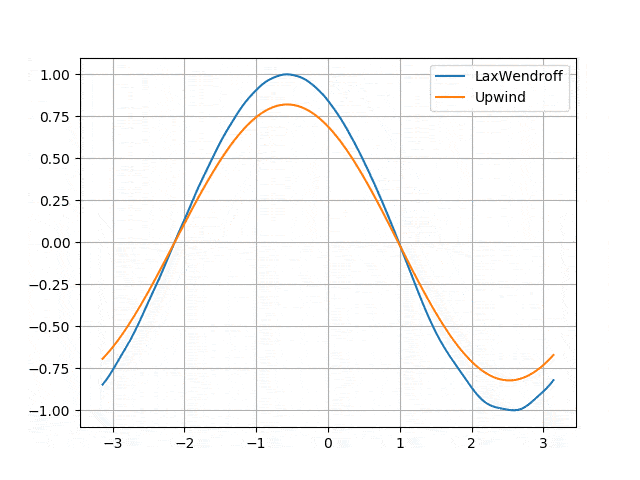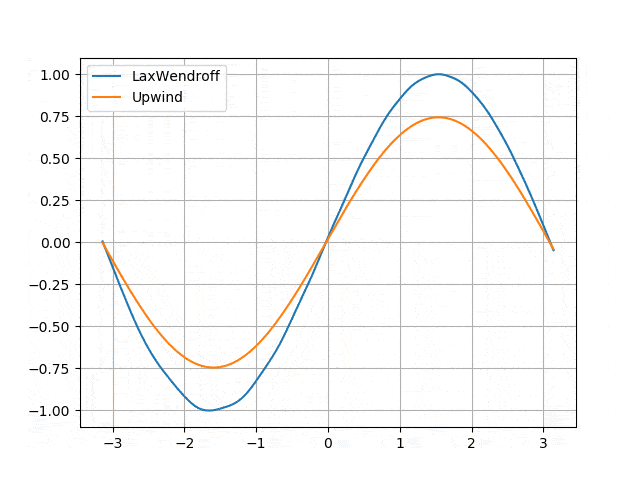 </p>
</p>
Parabolic: heat equation, advection-diffusion equation
- Numerical instability of Explicit Euler scheme <p align="center">
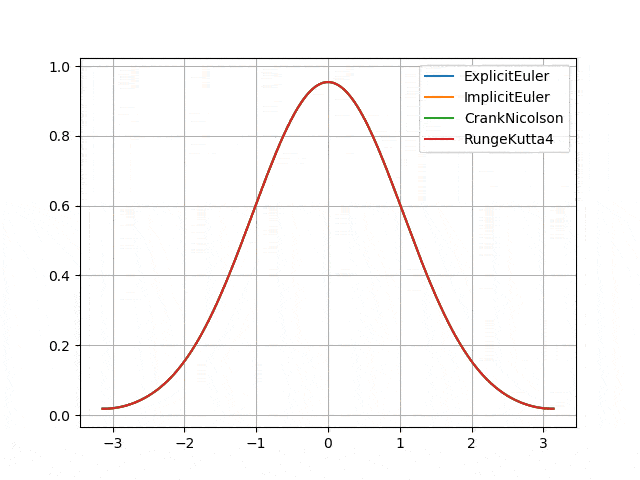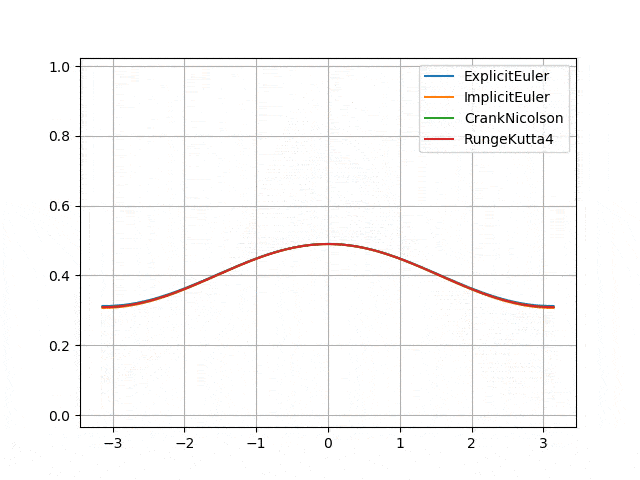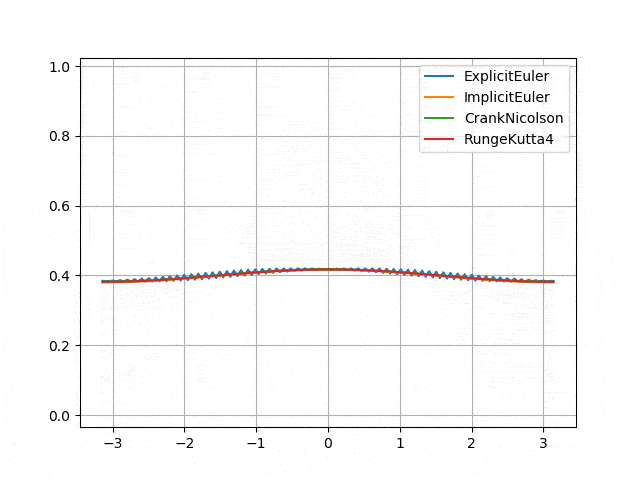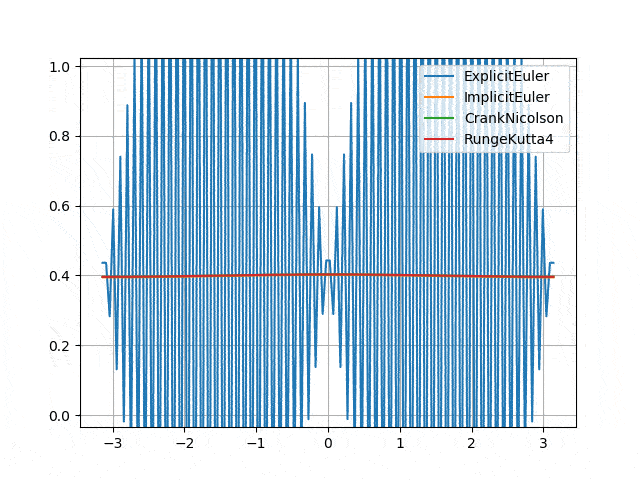 </p>
</p> - Numerical instability of Gauss-Legendre (4th order diagonally implicit Runge-Kutta) <p align="center">
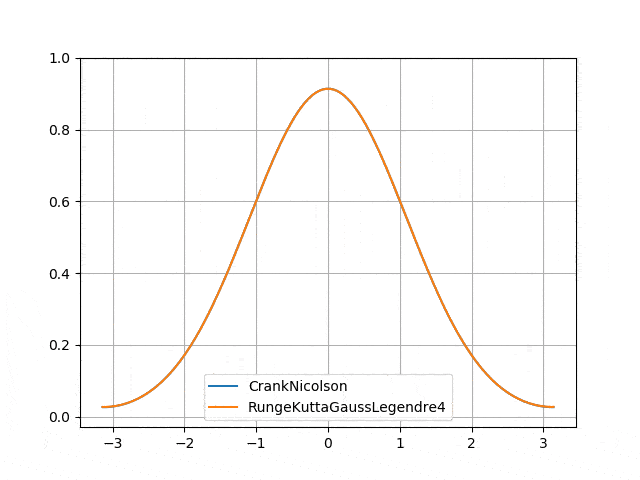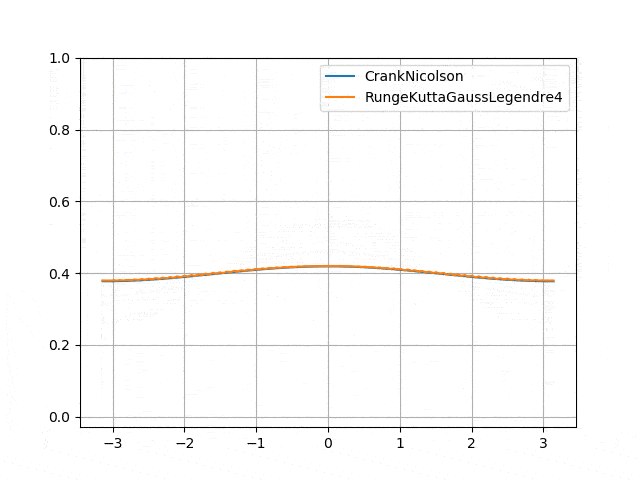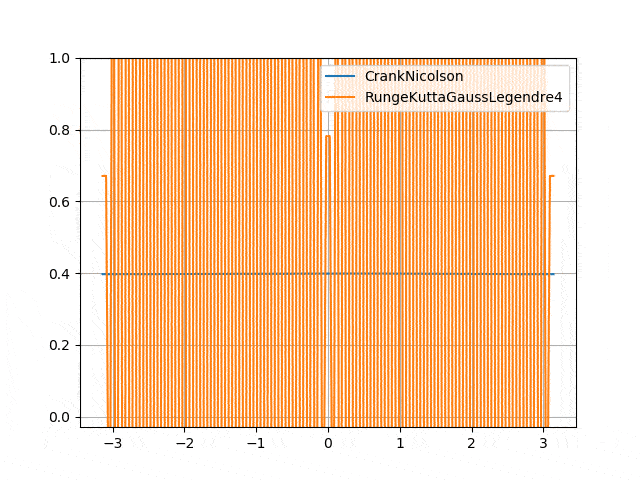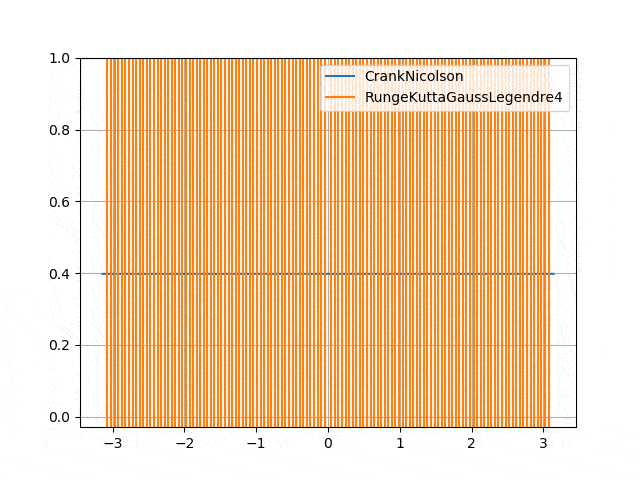 </p>
</p>
Hyperbolic - second order: wave equation
- Numerical instability of Implicit/Explicit Euler scheme <p align="center">
 </p>
</p>
Sample usage - 2D
Advection-Diffusion
cl::dvec xGrid = cl::LinSpace<MemorySpace::Device, MathDomain::Double>(0.0f, 1.0f, 32u);
cl::dvec yGrid = cl::LinSpace<MemorySpace::Device, MathDomain::Double>(0.0f, 1.0f, 32u);
double dt = 1e-5;
double xVelocity = .02;
double yVelocity = .05;
double diffusion = 1.0;
auto _xGrid = xGrid.Get();
auto _yGrid = yGrid.Get();
std::vector<double> _initialCondition(xGrid.size() * yGrid.size());
for (unsigned j = 0; j < _yGrid.size(); ++j)
for (unsigned i = 0; i < _xGrid.size(); ++i)
_initialCondition[i + _xGrid.size() * j] = exp(-_xGrid[i] * _xGrid[i] - _yGrid[i] * _yGrid[i]);
cl::dmat initialCondition(_initialCondition, xGrid.size(), yGrid.size());
pde::GpuDoublePdeInputData2D data(initialCondition, xGrid, yGrid, xVelocity, yVelocity, diffusion, dt, solverType, SpaceDiscretizerType::Centered, boundaryConditions);
pde::dad2D solver(data);
const auto solution = solver.solution->columns[0]->Get();
Wave Equation
cl::dvec xGrid = cl::LinSpace<MemorySpace::Device, MathDomain::Double>(0.0f, 1.0f, 32u);
cl::dvec yGrid = cl::LinSpace<MemorySpace::Device, MathDomain::Double>(0.0f, 1.0f, 32u);
double dt = 1e-5;
double xVelocity = .02;
auto _xGrid = xGrid.Get();
auto _yGrid = yGrid.Get();
std::vector<double> _initialCondition(xGrid.size() * yGrid.size());
for (unsigned j = 0; j < _yGrid.size(); ++j)
for (unsigned i = 0; i < _xGrid.size(); ++i)
_initialCondition[i + _xGrid.size() * j] = exp(-_xGrid[i] * _xGrid[i] - _yGrid[i] * _yGrid[i]);
cl::dmat initialCondition(_initialCondition, xGrid.size(), yGrid.size());
pde::GpuDoublePdeInputData2D data(initialCondition, xGrid, yGrid, xVelocity, 0.0, 0.0, dt, solverType, SpaceDiscretizerType::Centered, boundaryConditions);
pde::dwave2D solver(data);
const auto solution = solver.solution->columns[0]->Get();
Sample results - 2D
Hyperbolic - first order: transport equation
- Lax-Wendroff <p align="center">
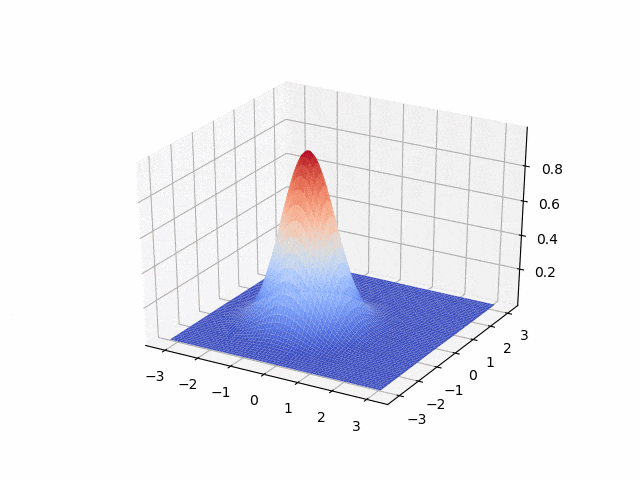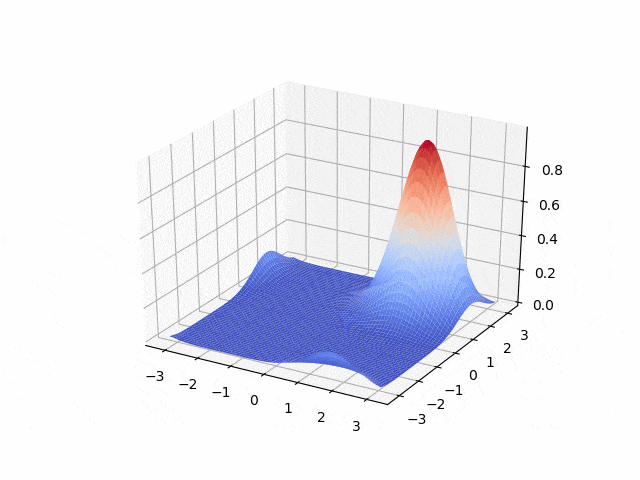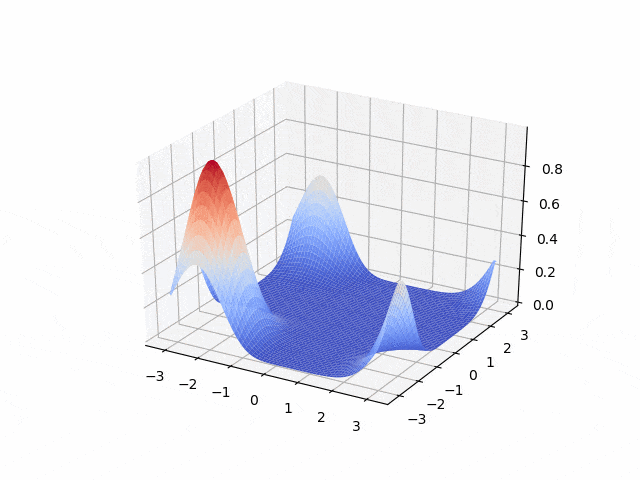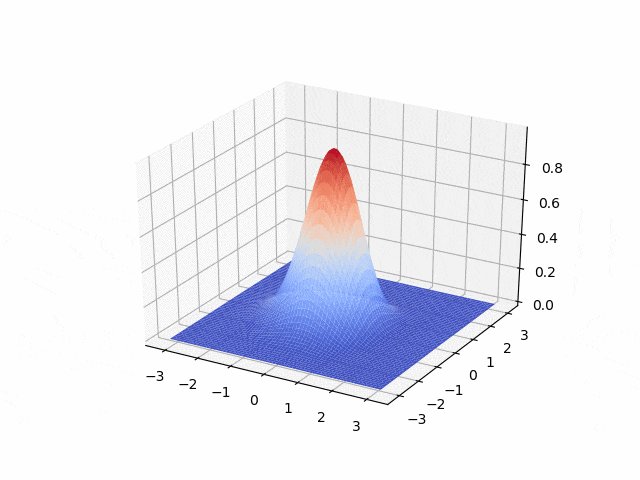 </p>
</p>
Parabolic: heat equation, advection-diffusion equation
- Crank-Nicolson <p align="center">
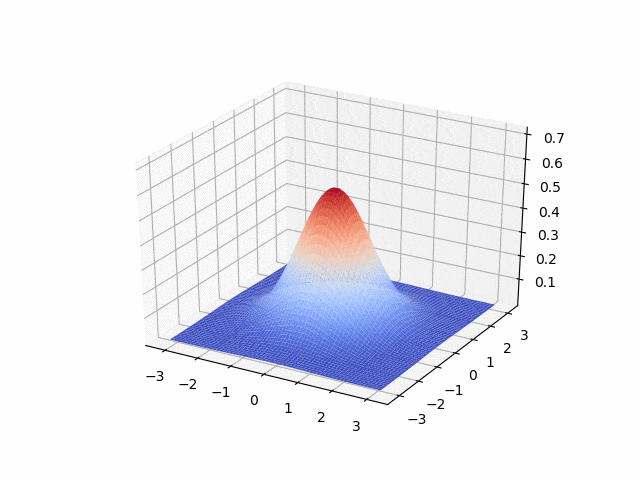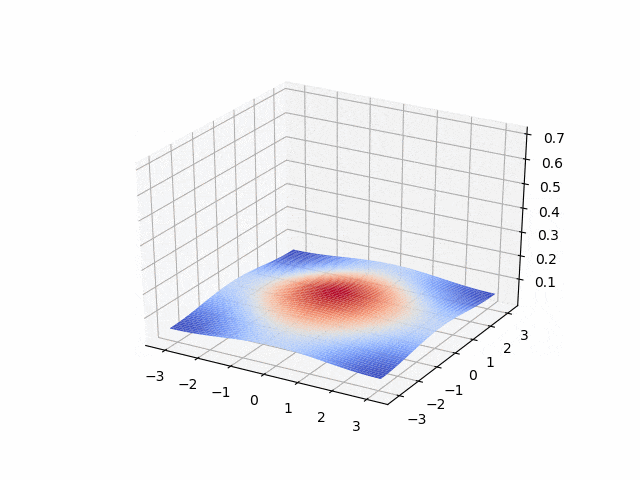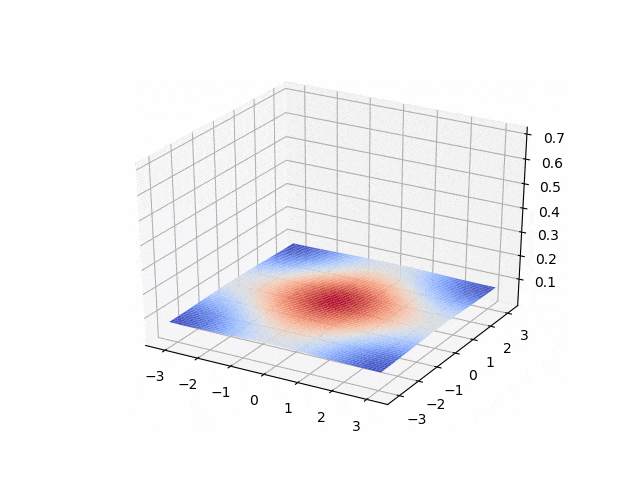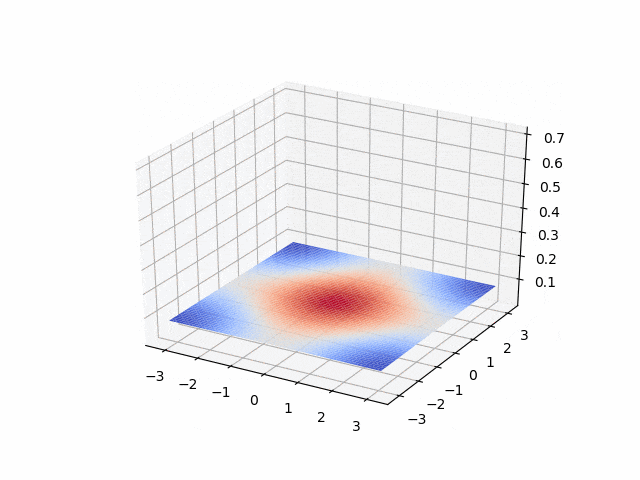 </p>
</p>
Hyperbolic - second order: wave equation
- Explicit Euler <p align="center">
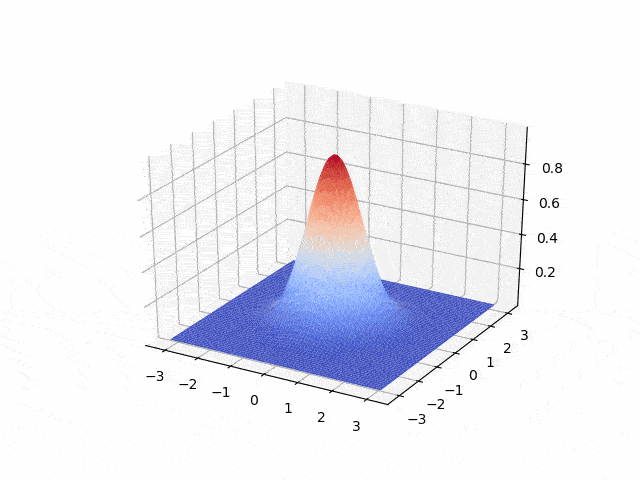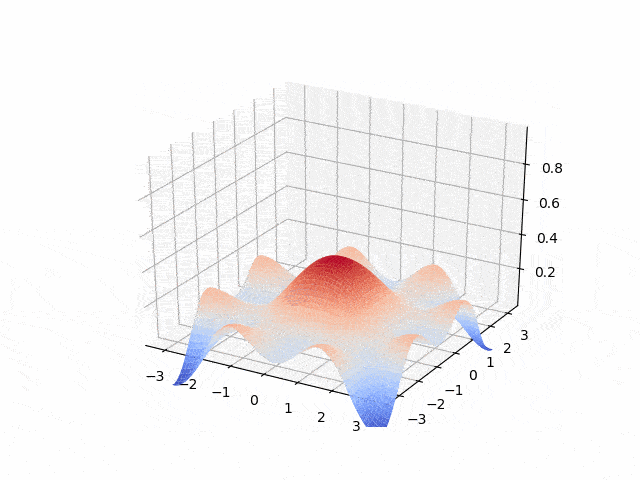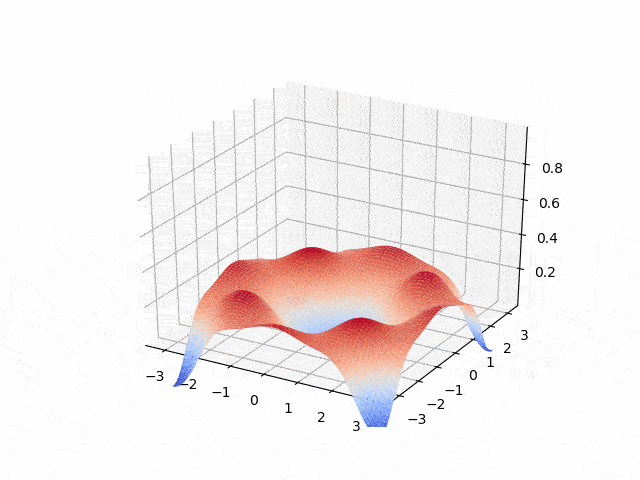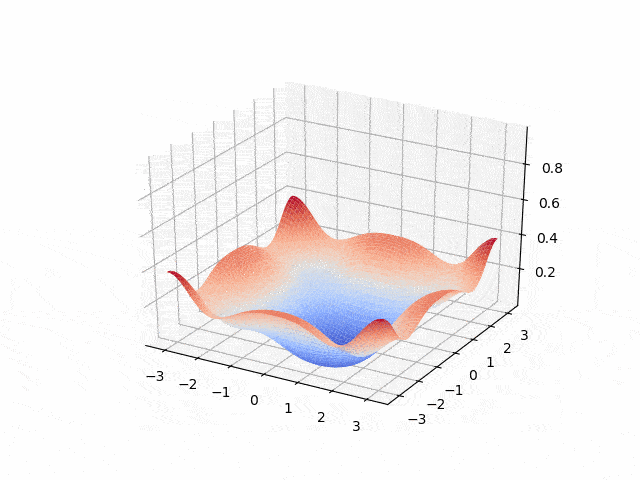 </p>
</p>